7.1 2nd Fundamental Theorem Of Calculusap Calculus

26-03-2021 admin

7.1 2nd Fundamental Theorem Of Calculus Ap Calculus Pdf
7.1 2nd Fundamental Theorem Of Calculus Ap Calculus Free
7.1 2nd Fundamental Theorem Of Calculus Ap Calculus Textbook
7.1 2nd Fundamental Theorem Of Calculus Ap Calculus Answers

In this wiki, we will see how the two main branches of calculus, differential and integral calculus, are related to each other. While the two might seem to be unrelated to each other, as one arose from the tangent problem and the other arose from the area problem, we will see that the fundamental theorem of calculus does indeed create a link between the two.

How do you use the second fundamental theorem of Calculus to find the derivative of given #int (2t-1)^3 dt# from #[x^2, x^7]#?

1 Answer

The derivative is #(2x^7-1)^3 (7x^6) - (2x^2-1)^3 (2x)#

Explanation:

7.1 2nd fundamental theorem of calculus ap calculus textbook

Suppose #f(x)# is continuous on #[a,b]# and both #p(x)# and #q(x)# are differentiable on #(a,b)#

4D2: 2nd Fundamental Theorem of Calculus The 1st Fundamental Theorem of Calculus defines a definite integral of 9(;) by its antiderivatives @(;). Now we will flip it around and define the function by its derivative. But first we will need a couple simple theorems regarding the area under a curve. First Fundamental Theorem of Calculus If ƒ(x) is continuous on a,b, then there is a c such that ∫(from a to b) ƒ(x) dx = ƒ(c)(b - a) Mean Value Theorem for Integrals.

Define the function

#F(x) = int_(p(x))^(q(x)) f(t) 'd't#

7.1 2nd Fundamental Theorem Of Calculusap Calculus

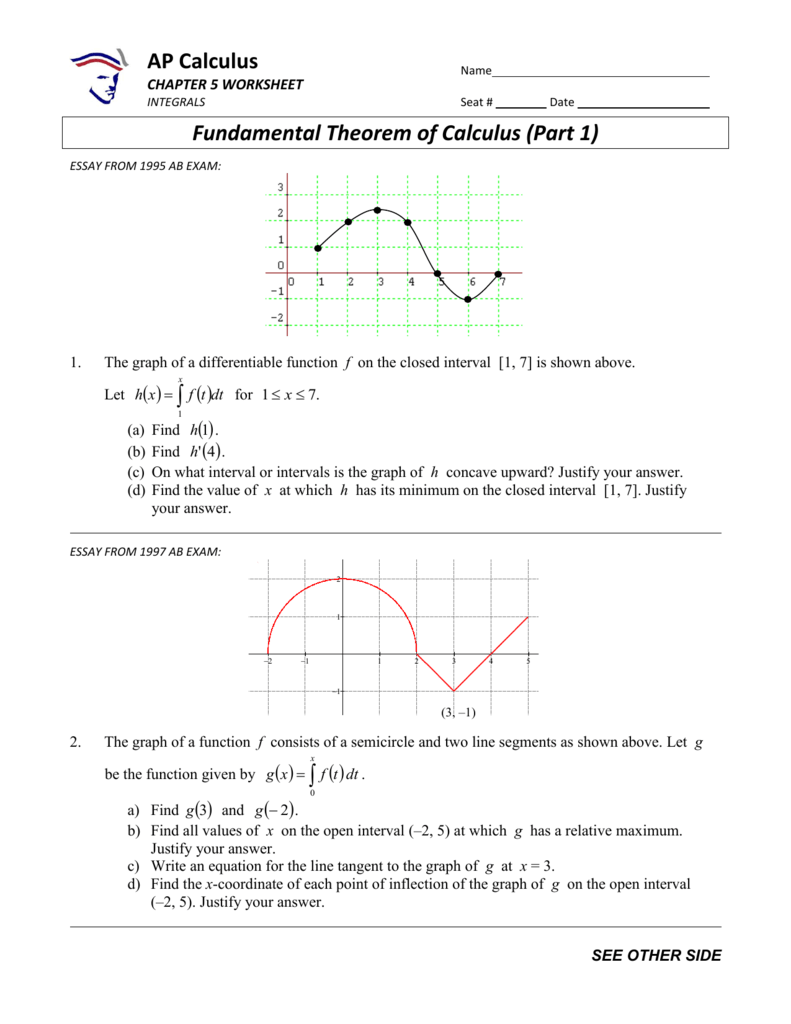
Combining the Second Fundamental Theorem of Calculus and the Chain Rule implies that #F(x)# is differentiable and

#F'(x) = f(q(x))*q'(x) - f(p(x))*p'(x)#

So, in this case we have

#f(t) = (2t-1)^3#
#p(x) = x^2#
#q(x) = x^7#

Plug it in to get

#frac{'d'}{'d'x}(int_(x^2)^(x^7) (2t-1)^3 'd't)#

# = (2(x^7)-1)^3 frac{'d'}{'d'x}(x^7) - (2(x^2)-1)^3 frac{'d'}{'d'x}(x^2)#

# = (2x^7-1)^3 (7x^6) - (2x^2-1)^3 (2x)#

Related questions

Let's recast the first example from the previous section. Suppose thatthe speed of the object is $3t$ at time $t$. How far does the objecttravel between time $t=a$ and time $t=b$? We are no longer assumingthat we know where the object is at time $t=0$ or at any othertime. It is certainly true that it is somewhere, so let'ssuppose that at $t=0$ the position is $k$. Then just as in theexample, we know that the position of the object at any time is $ds 3t^2/2+k$. This means that at time $t=a$ the position is $ds 3a^2/2+k$ and at time $t=b$ the position is $ds 3b^2/2+k$. Therefore thechange in position is $ds 3b^2/2+k-(3a^2/2+k)=3b^2/2-3a^2/2$. Notice thatthe $k$ drops out; this means that it doesn't matter that we don'tknow $k$, it doesn't even matter if we use the wrong $k$, we get thecorrect answer. In other words, to find the change in position betweentime $a$ and time $b$ we can use any antiderivative of thespeed function $3t$—it need not be the one antiderivative thatactually gives the location of the object.

What about the second approach to this problem, in the new form? Wenow want to approximate the change in position between time $a$ andtime $b$. We take the interval of time between $a$ and $b$, divide itinto $n$ subintervals, and approximate the distance traveled duringeach. The starting time of subinterval number $i$ is now $a+(i-1)(b-a)/n$, which we abbreviate as $ds t_{i-1}$, so that $ds t_0=a$, $ds t_1=a+(b-a)/n$, and so on. The speed of the object is$f(t)=3t$, and each subinterval is $(b-a)/n=Delta t$ seconds long.The distance traveled during subinterval number$i$ is approximately $ds f(t_{i-1})Delta t$, and the total change indistance is approximately$$ f(t_0)Delta t+f(t_1)Delta t+cdots+f(t_{n-1})Delta t.$$The exact change in position is the limit of this sum as $n$ goes toinfinity. We abbreviate this sum using sigma notation:$$ sum_{i=0}^{n-1} f(t_i)Delta t =f(t_0)Delta t+f(t_1)Delta t+cdots+f(t_{n-1})Delta t.$$The notation on the left side of the equal sign uses a large capitalsigma, a Greek letter, and the left side is an abbreviation for theright side. The answer we seek is$$ lim_{ntoinfty}sum_{i=0}^{n-1} f(t_i)Delta t.$$Since this must be the same as the answer we have already obtained, weknow that $$ lim_{ntoinfty}sum_{i=0}^{n-1} f(t_i)Delta t={3b^2over 2}-{3a^2over 2}.$$The significance of $ds 3t^2/2$, into which we substitute $t=b$ and$t=a$, is of course that it is a function whose derivative is $f(t)$.As we have discussed, by the time we know that we want to compute$$ lim_{ntoinfty}sum_{i=0}^{n-1} f(t_i)Delta t,$$it no longer matters what $f(t)$ stands for—it could be a speed, orthe height of a curve, or something else entirely. We know thatthe limit can be computed by finding any function with derivative$f(t)$, substituting $a$ and $b$, and subtracting. We summarize thisin a theorem. First, we introduce some new notation and terms.

We write$$ int_a^b f(t),dt = lim_{ntoinfty}sum_{i=0}^{n-1} f(t_i)Delta t$$ if the limit exists. That is, the left hand side means, or is anabbreviation for, the right hand side. The symbol $int$ is called anintegral sign, and the wholeexpression is read as 'the integral of $f(t)$ from $a$ to $b$.' Whatwe have learned is that this integral can be computed by finding afunction, say $F(t)$, with the property that $F'(t)=f(t)$, and thencomputing $F(b)-F(a)$. The function $F(t)$ is called an antiderivative of $f(t)$. Now the theorem:

Theorem 7.2.1 (Fundamental Theorem of Calculus) Suppose that $f(x)$ iscontinuous on the interval $[a,b]$. If $F(x)$ is any antiderivative of$f(x)$, then $$ int_a^b f(x),dx = F(b)-F(a).$$

Let's rewrite this slightly: $$ int_a^x f(t),dt = F(x)-F(a).$$We've replaced the variable $x$ by $t$ and $b$ by $x$. These are justdifferent names for quantities, so the substitution doesn't change themeaning. It does make it easier to think of the two sides of theequation as functions. The expression$$ int_a^x f(t),dt$$is a function: plug in a value for $x$, get out some other value. Theexpression $F(x)-F(a)$ is of course also a function, and it has a niceproperty: $$ {dover dx} (F(x)-F(a)) = F'(x) = f(x),$$since $F(a)$ is a constant and has derivative zero. In other words, byshifting our point of view slightly, we see that the odd lookingfunction$$ G(x)=int_a^x f(t),dt$$has a derivative, and that in fact $G'(x)=f(x)$. This is really just arestatement of the Fundamental Theorem of Calculus, and indeed isoften called the Fundamental Theorem of Calculus. To avoid confusion,some people call the two versions of the theorem 'The FundamentalTheorem of Calculus, part I' and 'The FundamentalTheorem of Calculus, part II', although unfortunately there is nouniversal agreement as to which is part I and which part II. Since itreally is the same theorem, differently stated, some people simplycall them both 'The FundamentalTheorem of Calculus.'

Theorem 7.2.2 (Fundamental Theorem of Calculus) Suppose that $f(x)$ iscontinuous on the interval $[a,b]$ and let$$ G(x)=int_a^x f(t),dt.$$Then $G'(x)=f(x)$.

We have not really proved the Fundamental Theorem. In a nutshell, wegave the following argument to justify it: Suppose we want to know thevalue of $$ int_a^b f(t),dt = lim_{ntoinfty}sum_{i=0}^{n-1} f(t_i)Delta t.$$We can interpret the right hand side as the distance traveled by anobject whose speed is given by $f(t)$. We know another way to computethe answer to such a problem: find the position of the object byfinding an antiderivative of $f(t)$, then substitute $t=a$ and $t=b$and subtract to find the distance traveled. This must be the answer tothe original problem as well, even if $f(t)$ does not represent aspeed.

What's wrong with this? In some sense, nothing. As a practical matterit is a very convincing argument, because our understanding of therelationship between speed and distance seems to be quite solid. Fromthe point of view of mathematics, however, it is unsatisfactory tojustify a purely mathematical relationship by appealing to ourunderstanding of the physical universe, which could, however unlikelyit is in this case, be wrong.

A complete proof is a bit too involved to include here, but we willindicate how it goes. First, if we can prove the second version of theFundamental Theorem, theorem 7.2.2, thenwe can prove the first version from that:

Proof of Theorem 7.2.1.
We know from theorem 7.2.2 that $$ G(x)=int_a^x f(t),dt$$is an antiderivative of $f(x)$, and therefore any antiderivative$F(x)$ of $f(x)$ is of the form $F(x)=G(x)+k$. Then $$eqalign{ F(b)-F(a)=G(b)+k-(G(a)+k) &= G(b)-G(a)cr &=int_a^b f(t),dt-int_a^a f(t),dt.cr}$$It is not hard to see that $ds int_a^a f(t),dt=0$, so this means that$$ F(b)-F(a)=int_a^b f(t),dt,$$which is exactly what theorem 7.2.1 says.

So the real job is to provetheorem 7.2.2. We will sketch the proof,using some facts that we do not prove. First, the following identityis true of integrals:$$ int_a^b f(t),dt = int_a^c f(t),dt + int_c^b f(t),dt.$$This can be proved directly from the definition of the integral, thatis, using the limits of sums. It is quite easy to see that it must betrue by thinking of either of the two applications of integrals thatwe have seen. It turns out that the identity is true no matter what$c$ is, but it is easiest to think about the meaning when $ale cle b$.

First, if $f(t)$ represents a speed, then we know that the threeintegrals represent the distance traveled between time $a$ and time $b$;the distance traveled between time $a$ and time $c$; and the distance traveled between time $c$ and time $b$. Clearly the sum ofthe latter two is equal to the first of these.

Second, if $f(t)$ represents the height of a curve, the threeintegrals represent the area under the curve between $a$ and $b$;the area under the curve between $a$ and $c$;and the area under the curve between $c$ and $b$. Again it is clearfrom the geometry that the first is equal to the sum of the second andthird.

Proof sketch forTheorem 7.2.2.
We want to compute $G'(x)$, so we start with the definition of thederivative in terms of a limit:$$eqalign{ G'(x)&=lim_{Delta xto0}{G(x+Delta x)-G(x)overDelta x}cr &=lim_{Delta xto0}{1over Delta x}left( int_a^{x+Delta x} f(t),dt - int_a^x f(t),dtright)cr &=lim_{Delta xto0}{1over Delta x}left( int_a^{x} f(t),dt + int_x^{x+Delta x} f(t),dt - int_a^x f(t),dtright)cr &=lim_{Delta xto0}{1over Delta x}int_x^{x+Delta x} f(t),dt.cr}$$Now we need to know something about $$ int_x^{x+Delta x} f(t),dt$$when $Delta x$ is small; in fact, it is very close to $Delta x f(x)$, but we will not prove this. Once again, it is easy tobelieve this is true by thinking of our two applications:The integral $$ int_x^{x+Delta x} f(t),dt$$can be interpreted as the distance traveled by an object over a veryshort interval of time. Over a sufficiently short period of time, thespeed of the object will not change very much, so the distancetraveled will be approximately the length of time multiplied by thespeed at the beginning of the interval, namely, $Delta xf(x)$. Alternately, the integral may be interpreted as the area underthe curve between $x$ and $x+Delta x$. When $Delta x$ is very small,this will be very close to the area of the rectangle with base $Deltax$ and height $f(x)$; again this is $Delta xf(x)$. If we accept this, we may proceed:$$ lim_{Delta xto0}{1over Delta x}int_x^{x+Delta x} f(t),dt =lim_{Delta xto0}{Delta x f(x)over Delta x}=f(x),$$which is what we wanted to show.

It is still true that we are depending on an interpretation of theintegral to justify the argument, but we have isolated this part ofthe argument into two facts that are not too hard to prove. Once thelast reference to interpretation has been removed from the proofs ofthese facts, we will have a real proof of the Fundamental Theorem.

Now we know that to solve certain kinds of problems, those that leadto a sum of a certain form, we 'merely' find an antiderivative andsubstitute two values and subtract. Unfortunately, findingantiderivatives can be quite difficult. While there are a small numberof rules that allow us to compute the derivative of any commonfunction, there are no such rules for antiderivatives. There are sometechniques that frequently prove useful, but we will never be able toreduce the problem to a completely mechanical process.

Because of the close relationship between an integral and anantiderivative, the integral sign is also used to mean'antiderivative'. You can tell which is intended by whether thelimits of integration are included:$$ int_1^2 x^2,dx$$is an ordinary integral, also called a definite integral,because it has a definite value, namely$$ int_1^2 x^2,dx={2^3over3}-{1^3over3}={7over3}.$$We use$$ int x^2,dx$$to denote the antiderivative of $ds x^2$, also called anindefinite integral.So this is evaluated as$$ int x^2,dx = {x^3over 3}+C.$$It is customary to include the constant $C$ to indicate that there arereally an infinite number of antiderivatives. We do not need this $C$to compute definite integrals, but in other circumstances we will needto remember that the $C$ is there, so it is best to get into the habitof writing the $C$.When we compute a definite integral, we first find an antiderivativeand then substitute. It is convenient to first display theantiderivative and then do the substitution; we need a notationindicating that the substitution is yet to be done. A typical solutionwould look like this:$$ int_1^2 x^2,dx=left.{x^3over 3}right|_1^2 = {2^3over3}-{1^3over3}={7over3}.$$The vertical line with subscript and superscript is used to indicatethe operation 'substitute and subtract' that is needed to finish theevaluation.

Exercises 7.2

Find the antiderivatives of the functions:

Ex 7.2.1$ds 8sqrt{x}$(answer)

Ex 7.2.2$ds 3t^2+1$(answer)

Ex 7.2.3$ds 4/sqrt{x}$(answer)

Ex 7.2.4$ds 2/z^2$(answer)

Ex 7.2.5$ds 7s^{-1}$(answer)

Ex 7.2.6$ds (5x+1)^2$(answer)

Ex 7.2.7$ds (x-6)^2$(answer)

Ex 7.2.8$ds x^{3/2}$(answer)

Ex 7.2.9$ds {2over xsqrt x}$(answer)

Ex 7.2.10$ds |2t-4|$(answer)

Compute the values of the integrals:

Ex 7.2.11$ds int_1^4 t^2+3t,dt$(answer)

Ex 7.2.12$ds int_0^pi sin t,dt$(answer)

Ex 7.2.13$ds int_1^{10} {1over x},dx$(answer)

Ex 7.2.14$ds int_0^5 e^x,dx$(answer)